
Qiyu Yang
Part 1: EDA
Insert cells as needed below to write a short EDA/data section that summarizes the data for someone who has never opened it before.
- Answer essential questions about the dataset (observation units, time period, sample size, many of the questions above)
- Note any issues you have with the data (variable X has problem Y that needs to get addressed before using it in regressions or a prediction model because Z)
- Present any visual results you think are interesting or important
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from statsmodels.formula.api import ols as sm_ols
from statsmodels.iolib.summary2 import summary_col # nicer tables
from eda import insufficient_but_starting_eda
import math
%matplotlib inline
housing = pd.read_csv("input_data2/housing_train.csv")
category variables:
category_columns = [col for col in housing.columns if housing[col].dtype == 'object']
print(category_columns)
['parcel', 'v_MS_Zoning', 'v_Street', 'v_Alley', 'v_Lot_Shape', 'v_Land_Contour', 'v_Utilities', 'v_Lot_Config', 'v_Land_Slope', 'v_Neighborhood', 'v_Condition_1', 'v_Condition_2', 'v_Bldg_Type', 'v_House_Style', 'v_Roof_Style', 'v_Roof_Matl', 'v_Exterior_1st', 'v_Exterior_2nd', 'v_Mas_Vnr_Type', 'v_Exter_Qual', 'v_Exter_Cond', 'v_Foundation', 'v_Bsmt_Qual', 'v_Bsmt_Cond', 'v_Bsmt_Exposure', 'v_BsmtFin_Type_1', 'v_BsmtFin_Type_2', 'v_Heating', 'v_Heating_QC', 'v_Central_Air', 'v_Electrical', 'v_Kitchen_Qual', 'v_Functional', 'v_Fireplace_Qu', 'v_Garage_Type', 'v_Garage_Finish', 'v_Garage_Qual', 'v_Garage_Cond', 'v_Paved_Drive', 'v_Pool_QC', 'v_Fence', 'v_Misc_Feature', 'v_Sale_Type', 'v_Sale_Condition']
continuous variables:
‘v_Lot_Frontage’, ‘v_Lot_Area’, ‘v_Mas_Vnr_Area’, ‘v_BsmtFin_F’_, ‘v_BsmtFin_SF_2’, ‘v_Bsmt_Unf_SF’, ‘v_Total_Bsmt_SF’, ‘v_1st_Flr_SF’, ‘v_2nd_Flr_SF’, ‘v_Low_Qual_Fin_SF’, ‘v_Gr_Liv_Area’, ‘v_Garage_Area’, ‘v_Wood_Deck_SF’, ‘v_Open_Porch_SF’, ‘v_Enclosed_Porch’, ‘v_3Ssn_Porch’, ‘v_Screen_Porch’, ‘v_Pool_Area’, ‘v_3Ssn_Porch’, ‘v_Screen_Porch’, ‘v_Pool_Area’, ‘v_Misc_Val’
# this is my testing code to see all graphs:
# continuous_vars = ['v_Lot_Frontage', 'v_Lot_Area', 'v_Mas_Vnr_Area', 'v_BsmtFin_SF_1' , 'v_BsmtFin_SF_2', 'v_Bsmt_Unf_SF', 'v_Total_Bsmt_SF', 'v_1st_Flr_SF',
# 'v_2nd_Flr_SF', 'v_Low_Qual_Fin_SF', 'v_Gr_Liv_Area', 'v_Garage_Area', 'v_Wood_Deck_SF', 'v_Open_Porch_SF', 'v_Enclosed_Porch',
# 'v_3Ssn_Porch', 'v_Screen_Porch', 'v_Pool_Area', 'v_3Ssn_Porch', 'v_Screen_Porch', 'v_Pool_Area', 'v_Misc_Val', 'v_SalePrice']
# for var in continuous_vars:
# plt.scatter(housing[var], housing['v_SalePrice'])
# plt.xlabel(var)
# plt.ylabel('v_SalePrice')
# plt.show()
num_rows = len(housing)
print("Number of observation units:", num_rows)
Number of observation units: 1941
min_date = housing["v_Year_Built"].min()
max_date = housing["v_Year_Built"].max()
period = (max_date - min_date)
print("Time period:", min_date, "to", max_date, "is", period)
Time period: 1872 to 2008 is 136
housing.shape
(1941, 81)
continuous_vars = ['v_Lot_Frontage', 'v_Lot_Area', 'v_Mas_Vnr_Area', 'v_BsmtFin_SF_1' , 'v_BsmtFin_SF_2', 'v_Bsmt_Unf_SF', 'v_Total_Bsmt_SF', 'v_1st_Flr_SF',
'v_2nd_Flr_SF', 'v_Low_Qual_Fin_SF', 'v_Gr_Liv_Area', 'v_Garage_Area', 'v_Wood_Deck_SF', 'v_Open_Porch_SF', 'v_Enclosed_Porch',
'v_3Ssn_Porch', 'v_Screen_Porch', 'v_Pool_Area', 'v_3Ssn_Porch', 'v_Screen_Porch', 'v_Pool_Area', 'v_Misc_Val', 'v_SalePrice']
insufficient_but_starting_eda(housing[continuous_vars], ['v_SalePrice'])
v_Lot_Frontage v_Lot_Area v_Mas_Vnr_Area v_BsmtFin_SF_1 v_BsmtFin_SF_2 \
0 107.0 13891 436.0 1400.0 0.0
1 98.0 12704 302.0 1012.0 0.0
2 114.0 14803 816.0 1636.0 0.0
3 126.0 13108 0.0 0.0 0.0
4 96.0 12444 426.0 1336.0 0.0
v_Bsmt_Unf_SF v_Total_Bsmt_SF v_1st_Flr_SF v_2nd_Flr_SF \
0 310.0 1710.0 1710 0
1 570.0 1582.0 1582 0
2 442.0 2078.0 2084 0
3 0.0 0.0 1226 0
4 596.0 1932.0 1932 0
v_Low_Qual_Fin_SF ... v_Open_Porch_SF v_Enclosed_Porch v_3Ssn_Porch \
0 0 ... 102 0 0
1 0 ... 95 0 0
2 0 ... 45 0 0
3 0 ... 24 120 0
4 0 ... 66 0 304
v_Screen_Porch v_Pool_Area v_3Ssn_Porch v_Screen_Porch v_Pool_Area \
0 0 0 0 0 0
1 0 0 0 0 0
2 0 0 0 0 0
3 228 0 0 228 0
4 0 0 304 0 0
v_Misc_Val v_SalePrice
0 0 372402
1 0 317500
2 0 385000
3 0 153500
4 0 394617
[5 rows x 23 columns]
---
v_Lot_Frontage v_Lot_Area v_Mas_Vnr_Area v_BsmtFin_SF_1 \
1936 79.0 13110 144.0 962.0
1937 NaN 7082 0.0 0.0
1938 60.0 10800 0.0 664.0
1939 55.0 5687 0.0 210.0
1940 60.0 12900 0.0 1300.0
v_BsmtFin_SF_2 v_Bsmt_Unf_SF v_Total_Bsmt_SF v_1st_Flr_SF \
1936 0.0 191.0 1153.0 1193
1937 0.0 686.0 686.0 948
1938 0.0 290.0 954.0 1766
1939 0.0 570.0 780.0 936
1940 0.0 0.0 1300.0 1140
v_2nd_Flr_SF v_Low_Qual_Fin_SF ... v_Open_Porch_SF v_Enclosed_Porch \
1936 0 0 ... 153 0
1937 980 0 ... 0 228
1938 648 0 ... 0 0
1939 780 0 ... 184 0
1940 0 0 ... 0 190
v_3Ssn_Porch v_Screen_Porch v_Pool_Area v_3Ssn_Porch v_Screen_Porch \
1936 0 0 0 0 0
1937 0 0 0 0 0
1938 0 0 0 0 0
1939 0 0 0 0 0
1940 0 0 0 0 0
v_Pool_Area v_Misc_Val v_SalePrice
1936 0 0 146500
1937 0 0 160000
1938 0 0 160000
1939 0 0 135900
1940 0 0 95541
[5 rows x 23 columns]
---
Index(['v_Lot_Frontage', 'v_Lot_Area', 'v_Mas_Vnr_Area', 'v_BsmtFin_SF_1',
'v_BsmtFin_SF_2', 'v_Bsmt_Unf_SF', 'v_Total_Bsmt_SF', 'v_1st_Flr_SF',
'v_2nd_Flr_SF', 'v_Low_Qual_Fin_SF', 'v_Gr_Liv_Area', 'v_Garage_Area',
'v_Wood_Deck_SF', 'v_Open_Porch_SF', 'v_Enclosed_Porch', 'v_3Ssn_Porch',
'v_Screen_Porch', 'v_Pool_Area', 'v_3Ssn_Porch', 'v_Screen_Porch',
'v_Pool_Area', 'v_Misc_Val', 'v_SalePrice'],
dtype='object')
---
The shape is: (1941, 23)
---
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1941 entries, 0 to 1940
Data columns (total 23 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 v_Lot_Frontage 1620 non-null float64
1 v_Lot_Area 1941 non-null int64
2 v_Mas_Vnr_Area 1923 non-null float64
3 v_BsmtFin_SF_1 1940 non-null float64
4 v_BsmtFin_SF_2 1940 non-null float64
5 v_Bsmt_Unf_SF 1940 non-null float64
6 v_Total_Bsmt_SF 1940 non-null float64
7 v_1st_Flr_SF 1941 non-null int64
8 v_2nd_Flr_SF 1941 non-null int64
9 v_Low_Qual_Fin_SF 1941 non-null int64
10 v_Gr_Liv_Area 1941 non-null int64
11 v_Garage_Area 1940 non-null float64
12 v_Wood_Deck_SF 1941 non-null int64
13 v_Open_Porch_SF 1941 non-null int64
14 v_Enclosed_Porch 1941 non-null int64
15 v_3Ssn_Porch 1941 non-null int64
16 v_Screen_Porch 1941 non-null int64
17 v_Pool_Area 1941 non-null int64
18 v_3Ssn_Porch 1941 non-null int64
19 v_Screen_Porch 1941 non-null int64
20 v_Pool_Area 1941 non-null int64
21 v_Misc_Val 1941 non-null int64
22 v_SalePrice 1941 non-null int64
dtypes: float64(7), int64(16)
memory usage: 348.9 KB
Info: None
---
v_Lot_Frontage v_Lot_Area v_Mas_Vnr_Area v_BsmtFin_SF_1 \
count 1620.000000 1941.000000 1923.000000 1940.000000
mean 69.301235 10284.770222 104.846074 436.986598
std 23.978101 7832.295527 184.982611 457.815715
min 21.000000 1470.000000 0.000000 0.000000
25% 58.000000 7420.000000 0.000000 0.000000
50% 68.000000 9450.000000 0.000000 361.500000
75% 80.000000 11631.000000 168.000000 735.250000
max 313.000000 164660.000000 1600.000000 5644.000000
v_BsmtFin_SF_2 v_Bsmt_Unf_SF v_Total_Bsmt_SF v_1st_Flr_SF \
count 1940.000000 1940.000000 1940.000000 1941.000000
mean 49.247938 567.437629 1053.672165 1161.071613
std 169.555232 439.600535 438.662147 396.945408
min 0.000000 0.000000 0.000000 334.000000
25% 0.000000 225.750000 796.750000 886.000000
50% 0.000000 474.000000 989.500000 1085.000000
75% 0.000000 815.000000 1295.250000 1383.000000
max 1474.000000 2153.000000 6110.000000 5095.000000
v_2nd_Flr_SF v_Low_Qual_Fin_SF ... v_Open_Porch_SF \
count 1941.000000 1941.000000 ... 1941.000000
mean 340.955178 4.282329 ... 49.157135
std 434.242152 42.943917 ... 70.296277
min 0.000000 0.000000 ... 0.000000
25% 0.000000 0.000000 ... 0.000000
50% 0.000000 0.000000 ... 28.000000
75% 717.000000 0.000000 ... 72.000000
max 2065.000000 697.000000 ... 742.000000
v_Enclosed_Porch v_3Ssn_Porch v_Screen_Porch v_Pool_Area \
count 1941.000000 1941.000000 1941.000000 1941.000000
mean 22.947965 2.249871 16.249871 3.386399
std 65.249307 22.416832 56.748086 43.695267
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 0.000000
75% 0.000000 0.000000 0.000000 0.000000
max 1012.000000 407.000000 576.000000 800.000000
v_3Ssn_Porch v_Screen_Porch v_Pool_Area v_Misc_Val v_SalePrice
count 1941.000000 1941.000000 1941.000000 1941.000000 1941.000000
mean 2.249871 16.249871 3.386399 52.553838 182033.238022
std 22.416832 56.748086 43.695267 616.064459 80407.100395
min 0.000000 0.000000 0.000000 0.000000 13100.000000
25% 0.000000 0.000000 0.000000 0.000000 130000.000000
50% 0.000000 0.000000 0.000000 0.000000 161900.000000
75% 0.000000 0.000000 0.000000 0.000000 215000.000000
max 407.000000 576.000000 800.000000 17000.000000 755000.000000
[8 rows x 23 columns]
---
v_SalePrice has 820 values and its top 10 most common are:
140000 26
135000 23
145000 21
130000 21
155000 18
120000 16
170000 15
250000 14
160000 14
127000 14
Name: v_SalePrice, dtype: int64
---
housing.describe()
| v_MS_SubClass | v_Lot_Frontage | v_Lot_Area | v_Overall_Qual | v_Overall_Cond | v_Year_Built | v_Year_Remod/Add | v_Mas_Vnr_Area | v_BsmtFin_SF_1 | v_BsmtFin_SF_2 | ... | v_Wood_Deck_SF | v_Open_Porch_SF | v_Enclosed_Porch | v_3Ssn_Porch | v_Screen_Porch | v_Pool_Area | v_Misc_Val | v_Mo_Sold | v_Yr_Sold | v_SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1941.000000 | 1620.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1923.000000 | 1940.000000 | 1940.000000 | ... | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 | 1941.000000 |
| mean | 58.088614 | 69.301235 | 10284.770222 | 6.113344 | 5.568264 | 1971.321999 | 1984.073158 | 104.846074 | 436.986598 | 49.247938 | ... | 92.458011 | 49.157135 | 22.947965 | 2.249871 | 16.249871 | 3.386399 | 52.553838 | 6.431221 | 2006.998454 | 182033.238022 |
| std | 42.946015 | 23.978101 | 7832.295527 | 1.401594 | 1.087465 | 30.209933 | 20.837338 | 184.982611 | 457.815715 | 169.555232 | ... | 127.020523 | 70.296277 | 65.249307 | 22.416832 | 56.748086 | 43.695267 | 616.064459 | 2.745199 | 0.801736 | 80407.100395 |
| min | 20.000000 | 21.000000 | 1470.000000 | 1.000000 | 1.000000 | 1872.000000 | 1950.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 2006.000000 | 13100.000000 |
| 25% | 20.000000 | 58.000000 | 7420.000000 | 5.000000 | 5.000000 | 1953.000000 | 1965.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 5.000000 | 2006.000000 | 130000.000000 |
| 50% | 50.000000 | 68.000000 | 9450.000000 | 6.000000 | 5.000000 | 1973.000000 | 1993.000000 | 0.000000 | 361.500000 | 0.000000 | ... | 0.000000 | 28.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 6.000000 | 2007.000000 | 161900.000000 |
| 75% | 70.000000 | 80.000000 | 11631.000000 | 7.000000 | 6.000000 | 2001.000000 | 2004.000000 | 168.000000 | 735.250000 | 0.000000 | ... | 168.000000 | 72.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 8.000000 | 2008.000000 | 215000.000000 |
| max | 190.000000 | 313.000000 | 164660.000000 | 10.000000 | 9.000000 | 2008.000000 | 2009.000000 | 1600.000000 | 5644.000000 | 1474.000000 | ... | 1424.000000 | 742.000000 | 1012.000000 | 407.000000 | 576.000000 | 800.000000 | 17000.000000 | 12.000000 | 2008.000000 | 755000.000000 |
8 rows × 37 columns
missing_values = housing.isna()
has_missing_values = missing_values.any()
# Use Boolean indexes to find columns containing missing values
columns_with_missing_values = housing.columns[has_missing_values].tolist()
columns_with_missing_values
['v_Lot_Frontage',
'v_Alley',
'v_Mas_Vnr_Type',
'v_Mas_Vnr_Area',
'v_Bsmt_Qual',
'v_Bsmt_Cond',
'v_Bsmt_Exposure',
'v_BsmtFin_Type_1',
'v_BsmtFin_SF_1',
'v_BsmtFin_Type_2',
'v_BsmtFin_SF_2',
'v_Bsmt_Unf_SF',
'v_Total_Bsmt_SF',
'v_Electrical',
'v_Bsmt_Full_Bath',
'v_Bsmt_Half_Bath',
'v_Fireplace_Qu',
'v_Garage_Type',
'v_Garage_Yr_Blt',
'v_Garage_Finish',
'v_Garage_Cars',
'v_Garage_Area',
'v_Garage_Qual',
'v_Garage_Cond',
'v_Pool_QC',
'v_Fence',
'v_Misc_Feature']
housing['v_SalePrice'].describe()
count 1941.000000
mean 182033.238022
std 80407.100395
min 13100.000000
25% 130000.000000
50% 161900.000000
75% 215000.000000
max 755000.000000
Name: v_SalePrice, dtype: float64
sns.displot(housing['v_SalePrice'])
<seaborn.axisgrid.FacetGrid at 0x1d508bce580>
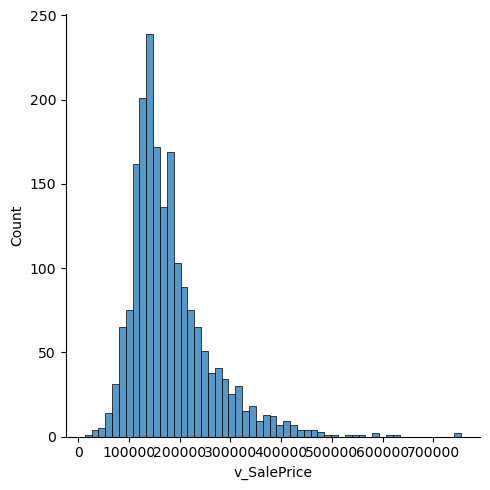
print("Skewness: %f" % housing['v_SalePrice'].skew())
print("Kurtosis: %f" % housing['v_SalePrice'].kurt())
Skewness: 1.770820
Kurtosis: 5.342356
saleprice is not a standard normal distribution, so subsequent processing of this data is required
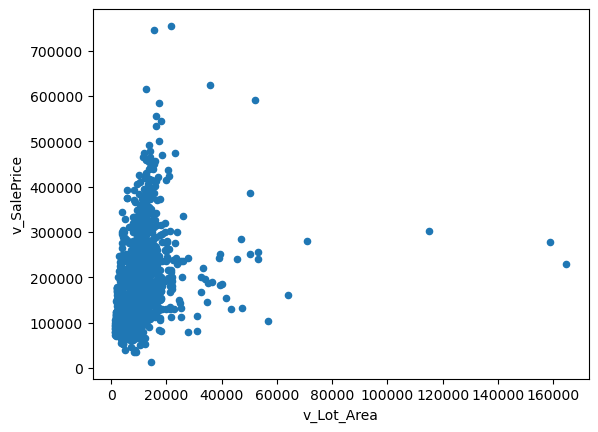
# The relationship between house price and area chart
var = 'v_Lot_Area'
data = pd.concat([housing['v_SalePrice'], housing[var]],axis=1)
data.plot.scatter(x=var, y='v_SalePrice')
D:\Anaconda3\lib\site-packages\pandas\plotting\_matplotlib\core.py:1114: UserWarning: No data for colormapping provided via 'c'. Parameters 'cmap' will be ignored
scatter = ax.scatter(
<AxesSubplot: xlabel='v_Lot_Area', ylabel='v_SalePrice'>
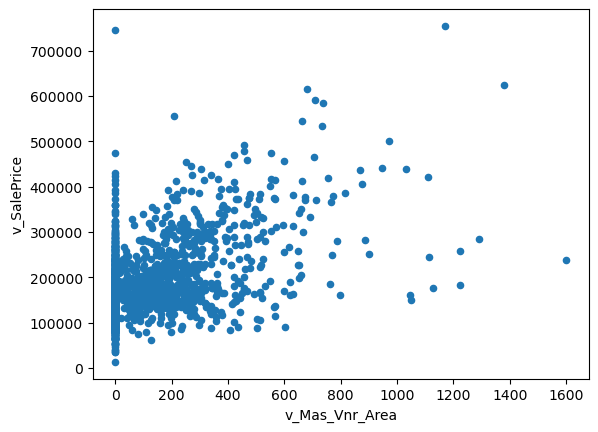
# The relationship between house price and area chart
var = 'v_Mas_Vnr_Area'
data = pd.concat([housing['v_SalePrice'], housing[var]],axis=1)
data.plot.scatter(x=var, y='v_SalePrice')
<AxesSubplot: xlabel='v_Mas_Vnr_Area', ylabel='v_SalePrice'>
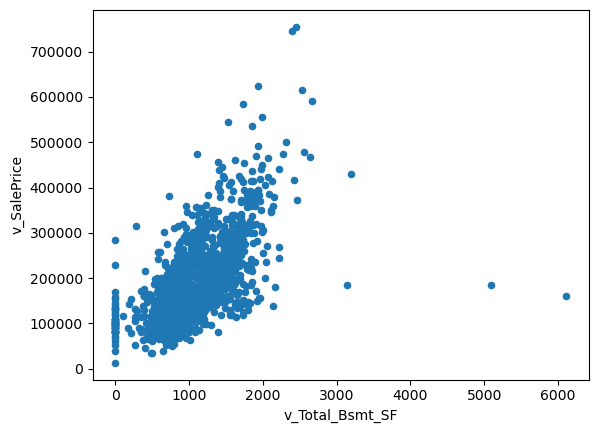
# The relationship between house price and basement area chart
var2 = 'v_Total_Bsmt_SF'
data = pd.concat([housing['v_SalePrice'], housing[var2]],axis=1)
data.plot.scatter(x=var2, y='v_SalePrice')
<AxesSubplot: xlabel='v_Total_Bsmt_SF', ylabel='v_SalePrice'>
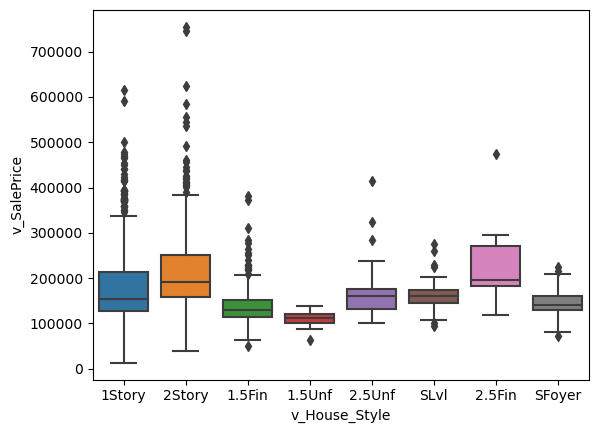
sns.boxplot(x='v_House_Style', y='v_SalePrice', data=housing)
<AxesSubplot: xlabel='v_House_Style', ylabel='v_SalePrice'>
PART 1: issues with data
-
First of all, we can see that there are missing data about many street information, housing structures such as basements, electrical settings, parking garages, etc. Some variables that in my opinion have little reference value can be disregarded if there are many missing values at the same time.
-
An observation of the house prices reveals that they still have the characteristics of a normal distribution, although there is a large skewness value of 1.77, which is not a standard normal distribution. I will address this issue for the purpose of subsequent forecasting.
-
A visual graph of the relationship between area and house price was selected for display. We can notice there are plenty of missing values and also it is reasonable that house price and area are directly proportional, but we can see some outlier points from the picture. Similarly, outliers were found when I examined the area of the basement
Part 2: Running Regressions
Run these regressions on the RAW data, even if you found data issues that you think should be addressed.
Insert cells as needed below to run these regressions. Note that $i$ is indexing a given house, and $t$ indexes the year of sale.
- $\text{Sale Price}_{i,t} = \alpha + \beta_1 * \text{v_Lot_Area}$
- $\text{Sale Price}_{i,t} = \alpha + \beta_1 * log(\text{v_Lot_Area})$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * \text{v_Lot_Area}$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * log(\text{v_Lot_Area})$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * \text{v_Yr_Sold}$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * (\text{v_Yr_Sold==2007})+ \beta_2 * (\text{v_Yr_Sold==2008})$
- Choose your own adventure: Pick any five variables from the dataset that you think will generate good R2. Use them in a regression of $log(\text{Sale Price}_{i,t})$
- Tip: You can transform/create these five variables however you want, even if it creates extra variables. For example: I’d count Model 6 above as only using one variable:
v_Yr_Sold. - I got an R2 of 0.877 with just “5” variables. How close can you get? I won’t be shocked if someone beats that!
- Tip: You can transform/create these five variables however you want, even if it creates extra variables. For example: I’d count Model 6 above as only using one variable:
Bonus formatting trick: Instead of reporting all regressions separately, report all seven regressions in a single table using summary_col.
Clean the data and create variables
housing = (housing
.assign(l_v_Lot_Area = np.log(housing['v_Lot_Area']),
l_v_SalePrice = np.log(housing['v_SalePrice'])
)
)
Statsmodels
model = sm_ols(<formula>, data=<dataframe>)
result=model.fit()
housing
| parcel | v_MS_SubClass | v_MS_Zoning | v_Lot_Frontage | v_Lot_Area | v_Street | v_Alley | v_Lot_Shape | v_Land_Contour | v_Utilities | ... | v_Fence | v_Misc_Feature | v_Misc_Val | v_Mo_Sold | v_Yr_Sold | v_Sale_Type | v_Sale_Condition | v_SalePrice | l_v_Lot_Area | l_v_SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1056_528110080 | 20 | RL | 107.0 | 13891 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 1 | 2008 | New | Partial | 372402 | 9.538996 | 12.827729 |
| 1 | 1055_528108150 | 20 | RL | 98.0 | 12704 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 1 | 2008 | New | Partial | 317500 | 9.449672 | 12.668233 |
| 2 | 1053_528104050 | 20 | RL | 114.0 | 14803 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 6 | 2008 | New | Partial | 385000 | 9.602585 | 12.860999 |
| 3 | 2213_909275160 | 20 | RL | 126.0 | 13108 | Pave | NaN | IR2 | HLS | AllPub | ... | NaN | NaN | 0 | 6 | 2007 | WD | Normal | 153500 | 9.480978 | 11.941456 |
| 4 | 1051_528102030 | 20 | RL | 96.0 | 12444 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 11 | 2008 | New | Partial | 394617 | 9.428994 | 12.885671 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1936 | 2524_534125210 | 190 | RL | 79.0 | 13110 | Pave | NaN | IR1 | Lvl | AllPub | ... | MnPrv | NaN | 0 | 7 | 2006 | WD | Normal | 146500 | 9.481131 | 11.894781 |
| 1937 | 2846_909131125 | 190 | RH | NaN | 7082 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 7 | 2006 | WD | Normal | 160000 | 8.865312 | 11.982929 |
| 1938 | 2605_535382020 | 190 | RL | 60.0 | 10800 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 5 | 2006 | ConLD | Normal | 160000 | 9.287301 | 11.982929 |
| 1939 | 1516_909101180 | 190 | RL | 55.0 | 5687 | Pave | Grvl | Reg | Bnk | AllPub | ... | NaN | NaN | 0 | 3 | 2008 | WD | Normal | 135900 | 8.645938 | 11.819675 |
| 1940 | 1387_905200100 | 190 | RL | 60.0 | 12900 | Pave | NaN | Reg | Lvl | AllPub | ... | NaN | NaN | 0 | 1 | 2008 | WD | Alloca | 95541 | 9.464983 | 11.467311 |
1941 rows × 83 columns
# one var: 'y ~ x' means fit y = a + b*X
reg1 = sm_ols('v_SalePrice ~ v_Lot_Area', data=housing).fit()
reg1b = sm_ols('v_SalePrice ~ l_v_Lot_Area', data=housing).fit()
reg2 = sm_ols('l_v_SalePrice ~ v_Lot_Area', data=housing).fit()
reg2b = sm_ols('l_v_SalePrice ~ l_v_Lot_Area', data=housing).fit()
reg2c = sm_ols('l_v_SalePrice ~ v_Yr_Sold', data=housing).fit()
reg2d = sm_ols('l_v_SalePrice ~ v_Yr_Sold==2007 + v_Yr_Sold==2008', data=housing).fit()
reg3 = sm_ols('l_v_SalePrice ~ v_Neighborhood + l_v_Lot_Area + v_Central_Air + v_Overall_Qual + v_1st_Flr_SF', data=housing).fit()
output them
info_dict = {'R-squared' : lambda x: f"{x.rsquared:.2f}",
'Adj R-squared' : lambda x: f"{x.rsquared_adj:.2f}",
'No. observations' : lambda x: f"{int(x.nobs):d}"}
print(summary_col(results=[reg1, reg1b, reg2, reg2b, reg2c, reg2d, reg3],
float_format='%0.4f',
stars = True,
model_names=['v_S1', 'v_S2', 'l_v_S1', 'l_v_S2', 'l_v_S3', 'l_v_S4', 'l_v_S5'],
info_dict = info_dict,
regressor_order=(['Intercept', 'v_SalePrice', 'v_Lot_Area', 'l_v_Lot_Area', 'l_v_SalePrice', 'v_Overall_Qual', 'v_Yr_Sold==2007 + v_Yr_Sold==2008', 'v_Neighborhood', 'v_1st_Flr_SF', 'v_Central_Air']
)))
=============================================================================================================
v_S1 v_S2 l_v_S1 l_v_S2 l_v_S3 l_v_S4 l_v_S5
-------------------------------------------------------------------------------------------------------------
Intercept 154789.5502*** -327915.8023*** 11.8941*** 9.4051*** 22.2932 12.0229*** 9.5884***
(2911.5906) (30221.3471) (0.0146) (0.1511) (22.9368) (0.0161) (0.0969)
v_Lot_Area 2.6489*** 0.0000***
(0.2252) (0.0000)
l_v_Lot_Area 56028.1700*** 0.2883*** 0.1481***
(3315.1392) (0.0166) (0.0109)
v_Overall_Qual 0.1454***
(0.0045)
v_1st_Flr_SF 0.0002***
(0.0000)
v_Neighborhood[T.Mitchel] -0.1745***
(0.0460)
v_Neighborhood[T.NPkVill] -0.1376**
(0.0692)
v_Neighborhood[T.NWAmes] -0.1308***
(0.0451)
v_Neighborhood[T.NoRidge] 0.1583***
(0.0477)
v_Neighborhood[T.NridgHt] 0.0710
(0.0438)
v_Neighborhood[T.OldTown] -0.2524***
(0.0432)
v_Neighborhood[T.SWISU] -0.1510***
(0.0525)
v_Neighborhood[T.SawyerW] -0.0972**
(0.0459)
v_Neighborhood[T.Sawyer] -0.2035***
(0.0448)
v_Neighborhood[T.Somerst] -0.0169
(0.0425)
v_Neighborhood[T.StoneBr] 0.0640
(0.0492)
v_Neighborhood[T.Timber] -0.0356
(0.0475)
v_Neighborhood[T.Veenker] -0.0629
(0.0564)
v_Yr_Sold -0.0051
(0.0114)
v_Yr_Sold == 2007[T.True] 0.0256
(0.0222)
v_Neighborhood[T.NAmes] -0.2019***
(0.0423)
v_Neighborhood[T.MeadowV] -0.1611***
(0.0531)
v_Neighborhood[T.ClearCr] -0.0639
(0.0529)
v_Neighborhood[T.Landmrk] -0.1119
(0.1765)
v_Central_Air[T.Y] 0.1704***
(0.0173)
v_Neighborhood[T.Blueste] -0.0709
(0.0945)
v_Neighborhood[T.BrDale] -0.2530***
(0.0547)
v_Neighborhood[T.BrkSide] -0.2447***
(0.0454)
v_Yr_Sold == 2008[T.True] -0.0103
(0.0228)
v_Neighborhood[T.CollgCr] -0.0794*
(0.0425)
v_Neighborhood[T.Crawfor] -0.0200
(0.0452)
v_Neighborhood[T.Edwards] -0.2451***
(0.0438)
v_Neighborhood[T.Gilbert] -0.0819*
(0.0448)
v_Neighborhood[T.Greens] -0.1468*
(0.0862)
v_Neighborhood[T.GrnHill] 0.1903
(0.1279)
v_Neighborhood[T.IDOTRR] -0.3619***
(0.0463)
R-squared 0.0666 0.1284 0.0646 0.1350 0.0001 0.0014 0.8214
R-squared Adj. 0.0661 0.1279 0.0641 0.1345 -0.0004 0.0004 0.8185
R-squared 0.07 0.13 0.06 0.13 0.00 0.00 0.82
Adj R-squared 0.07 0.13 0.06 0.13 -0.00 0.00 0.82
No. observations 1941 1941 1941 1941 1941 1941 1941
=============================================================================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
Part 3: Regression interpretation
Insert cells as needed below to answer these questions. Note that $i$ is indexing a given house, and $t$ indexes the year of sale.
- If you didn’t use the
summary_coltrick, list $\beta_1$ for Models 1-6 to make it easier on your graders. - Interpret $\beta_1$ in Model 2.
- Interpret $\beta_1$ in Model 3.
- HINT: You might need to print out more decimal places. Show at least 2 non-zero digits.
- Of models 1-4, which do you think best explains the data and why?
- Interpret $\beta_1$ In Model 5
- Interpret $\alpha$ in Model 6
- Interpret $\beta_1$ in Model 6
- Why is the R2 of Model 6 higher than the R2 of Model 5?
- What variables did you include in Model 7?
- What is the R2 of your Model 7?
- Speculate (not graded): Could you use the specification of Model 6 in a predictive regression?
- Speculate (not graded): Could you use the specification of Model 5 in a predictive regression?
beta1 = reg1.params[1]
beta2 = reg1b.params[1]
beta3 = reg2.params[1]
beta4 = reg2b.params[1]
beta5 = reg2c.params[1]
beta6a = reg2d.params[1]
beta6b = reg2d.params[2]
print("beta1:", beta1)
print("beta2:",beta2)
print("beta3:",beta3)
print("beta4:",beta4)
print("beta5:",beta5)
print("beta6a:",beta6a)
print("beta6b:",beta6b)
beta1: 2.64893500071819
beta2: 56028.16996046535
beta3: 1.3092338465836551e-05
beta4: 0.28826331962293267
beta5: -0.005114348195977281
beta6a: 0.02559031997164772
beta6b: -0.010281565074485799
# Interpret $\beta_1$ in Model 2.
change2 = beta2/100
print("if v_Lot_Area increase 1%, then saleprice increase by about", change2)
if v_Lot_Area increase 1%, then saleprice increase by about 560.2816996046535
# Interpret $\beta_1$ in Model 3.
beta3_percentage = "{:.4%}".format(beta3)
print("if v_Lot_Area increase by 1 unit, then saleprice increase by about", beta3_percentage)
if v_Lot_Area increase by 1 unit, then saleprice increase by about 0.0013%
Of models 1-4, which do you think best explains the data and why?
I think model 4 is the best explainable model because:
- In general, the beta value should be between 0 and 1. Too big is too extreme.
- R^2 the closer to 1 means the better the model fits the data. Therefore, model 4 has the highest value contrast with others.
# Interpret $\beta_1$ In Model 5
beta5_percentage = "{:.4%}".format(beta5)
print("if v_Lot_Area increase by 1 unit, then saleprice increase by about", beta5_percentage)
if v_Lot_Area increase by 1 unit, then saleprice increase by about -0.5114%
# Interpret $\alpha$ in Model 6
alpha6 = reg2d.params[0].mean()
print("the average value of log of saleprice if X=0, alpha =", f"{alpha6:.4f}")
the average value of log of saleprice if X=0, alpha = 12.0229
# Interpret $\beta_1$ in Model 6
beta6_percentage = "{:.4%}".format(beta6a)
print("when the year is in 2007, the sale price is about ", beta6_percentage, "higher")
when the year is in 2007, the sale price is about 2.5590% higher
Why is the R2 of Model 6 higher than the R2 of Model 5?
One possibility is that the relationship between year and home sales price may show a nonlinear trend, such as showing an accelerating or slowing rate of change in year, and this nonlinear trend may make the linearity assumption of the first model too simple to explain well the variability of the dependent variable. The second model, on the other hand, introduces two dummy variables that may better fit this nonlinear trend, resulting in a larger R-squared value.
What variables did you include in Model 7?
I selected ‘v_Neighborhood + l_v_Lot_Area + v_Central_Air + v_Overall_Qual + v_1st_Flr_SF’
What is the R2 of your Model 7?
0.8214
Speculate (not graded): Could you use the specification of Model 6 in a predictive regression?
Speculate (not graded): Could you use the specification of Model 5 in a predictive regression?
I don’t think these two models are predictive. First of all, the selected variables are too few to be informative, and the data are not preprocessed and there are too many null values, and then the data are too few to divide the data for training and testing the model.